Heap is a binary tree.
Heap can have duplicates.
max heap
min heap
max heap, min heap이 있다.
binary tree 형태를 가지고 있다.
중복값이 있을 수 있다.
부모노드들 중 하나보다 작기만 해도 됨.
힙을 어레이구조로 저장한다고 하면
맨 위 노드가 index 1, 2번째 줄 왼쪽노드 index 2, 오른쪽 노드 index 3 …
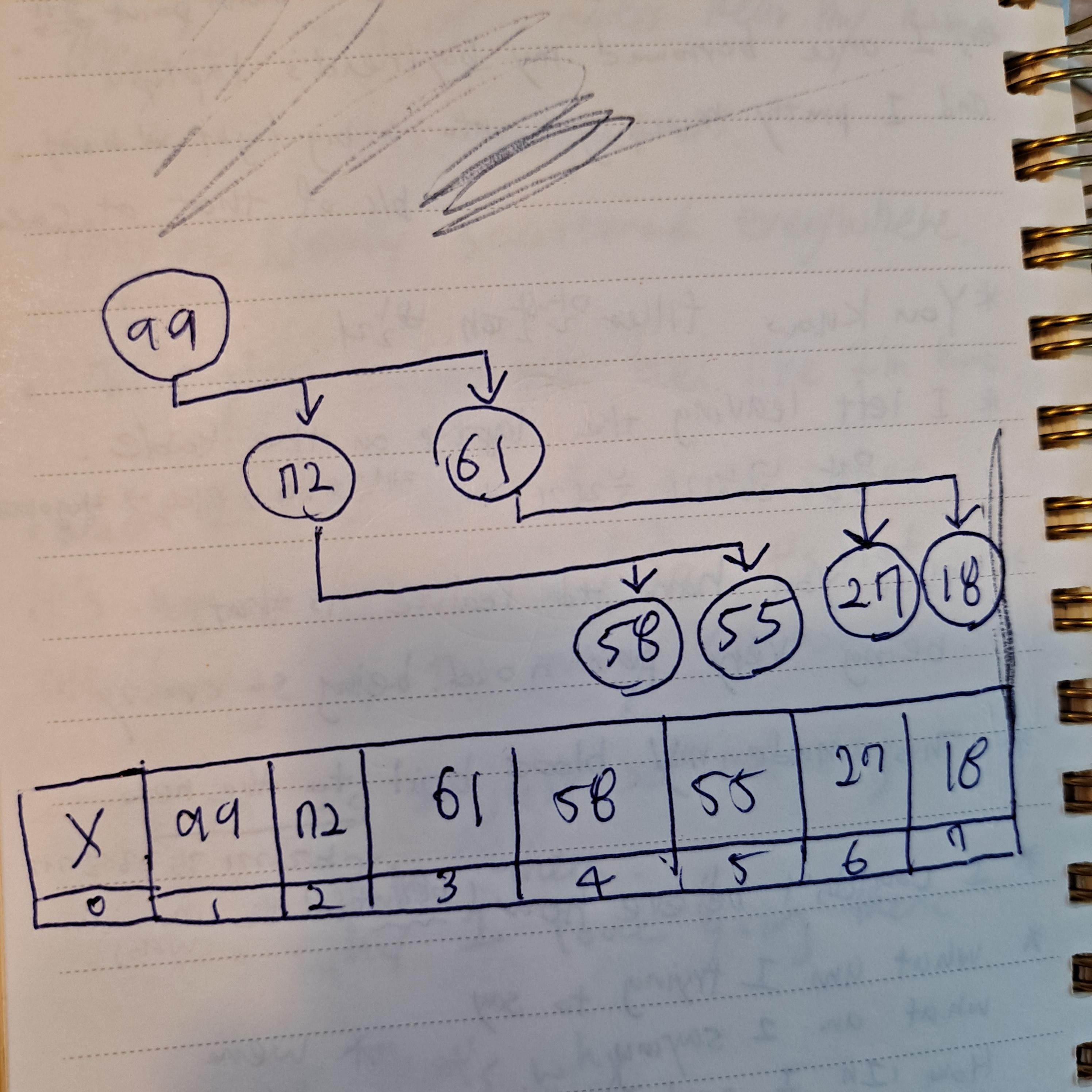
이런식으로 순차적으로 저장된다.
- 이 상황에서 노드의 자식들을 구하려면
leftChild = 2 * parentIndex
rightChild = 2 * parentIndex + 1
결과 값은 계산에 적용된 부모노드의 왼쪽노드 오른쪽 노드의 인덱스 값이다.
- 반대로 노드의 부모노드를 찾기 위해서는
2로 나누면 되겠지. 나머지는 버림
Insert
- 새로운 노드를 삽입하는데 처음엔 complete 조건에 맞게 왼쪽부터 차례대로 삽입한다.
- 근데 새로 삽입된 노드의 값이 부모값보다 크다면 둘을 바꾼다.
- 바꾼 후에도 바꾼자리에서의 부모의 값보다 크다면 또 바꾼다.
public void insert(Integer value){
//새로운 노드 마지막 인덱스에 추가
heap.add(value);
//새로운 노드의 인덱스 값
int current = heap.size() - 1;
//새로운 노드가 첫번째 노드가 아니고, 새로운 노드의 값이 부모노드의 값보다 클때.
while(current > 0 && heap.get(current) > heap.get(parent(current))){
//새로운 노드와 부모의 값을 맞바꾼다.
swap(current,parent(current));
//부모와 자리를 바꿨으니 새로운 노드의 인덱스 값을 부모 인덱스로 업데이트 한다.
current = parent(current);
}
}
remove
heap 자료구조는 선입선출이다.
그래서 remove 하면 제일 첫 번째 인덱스에 있는 노드가 삭제되어야 한다.
트리구조의 힙에서 맨 위의 노드가 없어지면 트리는 불완정한 상태가 된다.
최소한의 스텝으로 complete 상태가 되게 하려면 맨 마지막 노드를 맨 처음으로 옮기면 된다.
그렇게 되면 맨 위의 노드의 값이 제일 커야 하는데 맨 마지막 노드를 위로 옮기게 되면 그 조건이 충족되지 못하는 상태가 될 수도 있다.
맨 아래 노드를 맨 위로 옮긴 후 자식들과 값을 비교해서 작으면 점점 내려가게 하는 sink down 메서드를 이용한다.
public Integer remove(){
if(heap.size() == 0){
return null;
}
if(heap.size()==1){
return heap.remove(0);
}
int maxVal = heap.get(0);
heap.set(0,heap.remove(heap.size()-1));
sinkDown(0);
return maxVal;
}
sink down
맨 위의 노드를 값에 따라 알맞은 위치로 내리는 메서드
이 메서드는 애초에 맨 위의 노드를 알맞은 자리로 내리는 역할을 하기 때문에 따로 인덱스값을 받을 필요는 없지만 그냥 받음
public void sinkDown(int index){
int maxIndex = index;
while(true){
//자식들 값 비교하기위해 변수에 저장
int leftIndex = leftChild(index);
int rightIndex = rightChild(index);
if(leftIndex < heap.size() && heap.get(maxIndex) < heap.get(leftIndex)){
maxIndex = leftIndex;
}
if(rightIndex < heap.size() && heap.get(maxIndex) < heap.get(rightIndex)){
maxIndex = rightIndex;
}
//자식들의 값이 더 커서 maxIndex값이 바꼈을 경우.
if(index != maxIndex){
//더 큰 자식값과 값 바꿔치기
int temp = heap.get(index);
heap.set(index,heap.get(maxIndex));
heap.set(maxIndex,temp);
//다음 반복문을 위해 시작 위치 변경
index = maxIndex;
}else{
//index값과 maxIndex값이 같은 경우 자식들중에 더 큰 값이 없다는 뜻이므로 리턴.
return;
}
}
}'study > Data structure' 카테고리의 다른 글
| Graph (0) | 2023.09.03 |
|---|---|
| HashTable (0) | 2023.08.27 |
| Trees (0) | 2023.08.17 |
| stack and queue (0) | 2023.08.11 |
| Doubly linked list (0) | 2023.08.04 |




댓글